Polygon (MATIC) a commencé à montrer des signes de reprise après une forte correction au cours de la dernière semaine environ. La baisse des prix fait partie d’un effondrement plus large du marché au sens large, mais MATIC semble se consolider pour sa prochaine étape. Voici les principaux faits :
-
MATIC a réussi à maintenir le support de 0,8 $ malgré une pression de vente massive.
-
La pièce peut récupérer l’important prix psychologique de 1 $ dans les jours à venir.
-
Cela pourrait déclencher une tendance haussière qui pourrait générer au moins 25 % de gains.
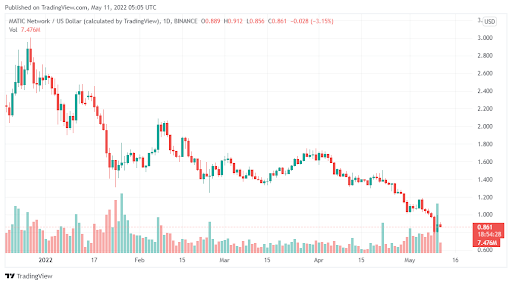Source des données : Tradingview
Polygone (MATIC) – prévision des prix
Après avoir atteint un nouveau sommet de 1,73 $ en 2022, MATIC a perdu une grande partie de son élan ascendant. La pièce a chuté au cours des deux dernières semaines, perdant plusieurs supports clés dans le processus. La plus grande inquiétude des taureaux est cependant survenue après que le jeton soit tombé en dessous du prix psychologique crucial de 1 $.
Mais malgré cette pression de vente, MATIC semble avoir trouvé un support solide à 0,8 $. La pièce a maintenu ce niveau alors même que le marché au sens large se vend. C’est un bon signe, en fait, nous assistons actuellement à une consolidation autour de 0,8 $. Si cela continue, MATIC va probablement récupérer le prix de 1 $.
Après cela, les haussiers peuvent prendre le relais et faire grimper l’action des prix d’au moins 25 % par rapport au prix de 1 $. En outre, les indicateurs de momentum, y compris le RSI, montrent une divergence haussière qui pourrait pousser le prix encore plus haut.
Comment profiter de cette configuration ?
MATIC a déjà chuté massivement par rapport à ses sommets de 2022. Si vous avez toujours voulu posséder cet altcoin, c’est le moins cher depuis un moment. C’est donc un bon moment pour acheter, surtout pour les investisseurs à long terme.
En ce qui concerne le jeu à court terme, une bonne approche serait d’attendre que l’altcoin récupère 1 $. Une fois que cela se produit, vous pouvez acheter et sortir à environ 1,3 $.